1
-
-
-
企業ニュース
アクセスランキング-
-
2
-
3
-
4
-
5
-
6
-
7
-
8
-
9
-
10
働きやすい企業ランキング
-
統計のウソに騙されるな！ 恐ろしい「シンプソンのパラドクス」を知っておこう
ビジネスに活用できる実践的な知識として、「統計学」がブームだ。
東大医学部卒の統計専門家、西内啓氏の『統計学が最強の学問である』はベストセラーになった。「週刊ダイヤモンド」も「最強の武器『統計学』」と題した特集を展開し、売り上げ好調だったという。
統計学を身につけていれば、仕事の幅も広がる。多変量解析などの知識と技術は、業種や職種を問わず応用範囲が広いし、仮説を統計的に検証するカイ２乗検定やｔ検定といった手法は、マーケティングの現場でも使われる。
そればかりではない。統計学を理解すれば、他人から騙されにくくなる。逆に言えば、統計学を知らない人を騙すことは容易なのである。その典型例のひとつが「シンプソンのパラドクス」だ。
米国の統計学者E. H. シンプソンが提示した「集団を2つに分けた場合にある仮説が成立しても、集団全体では正反対の仮説が成立することもある」という統計学的なパラドックスのことである。
例えば、Ａ高校とＢ高校の成績を比べてみよう。次のような場合、全体の平均点が高いのはどちらだろうか？
・男子の平均点は、Ａ高校がＢ高校より５点高かった。
・女子の平均も、Ａ高校がＢ高校より５点高かった。
統計学を知らなければ、「そりゃＡ高校でしょ」と即断してしまうが、正しくは「これだけでは、どちらか分からない」のである。
なぜだろうか。西内氏が著書で挙げている例をもとに、具体的な平均点を見ていくと、男子のＡ高校は１６０人で６０点、Ｂ高校は４０人で５５点。次に女子を見ると、Ａ高校は４０人で７５点、Ｂ高校は１６０人で７０点だったとする。
男子も女子もＡ高校のほうが平均点が高いが、それぞれの得点計をもとに、全体の平均点を計算するとどうなるだろうか。表からも一目瞭然だが、なんとＢ高校の平均点のほうが4点も高くなるのだ。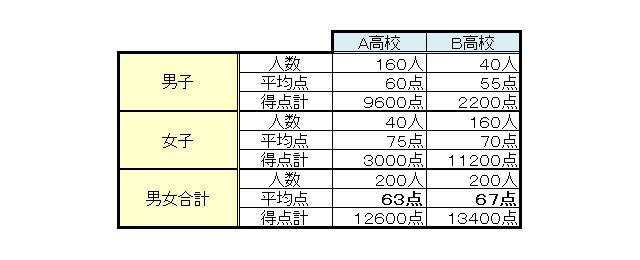
経営会議に間違った分析資料を出したら大変だ
これは数学的には「加重平均」という処理の差によるものである。Ａ高校もＢ高校も、それぞれの高校内で平均点を比べると、女子の方が高い。その好成績に寄与している女子がＢ高校のほうが多いから、本来ならばＢ高校により多くの「加重」をしなければならない。
ところが、この知識がないと、最初の問題文を読んだだけで「単純平均」をイメージしてしまうために、正解を誤るのである。
このことは、たとえば医師の治療成績などを比較するときに、より深刻な問題をもたらす。Ａ高校とＢ高校を、それぞれＡ医師とＢ医師、あるいはＡ病院とＢ病院に置き換えてみると容易に想像できるだろう。
肝臓の治療成績を比較すると、Ａ医師はＢ医師より成績がよかった。腎臓の治療成績を見ても、Ａ医師はＢ医師より成績がよかった。このことから、Ａ医師はＢ医師よりも優秀だと言えるだろうか。
答えはもちろんＮＯである。全体を平均すると、Ｂ医師のほうが治療成績は高くなることもある。
うっかり勘違いを元に他人を批判して、恥ずかしい思いをしないようにしたいし、経営上の意思決定の場に間違った資料を提出して、会社を危険に晒さないようにしたい。もちろん、わざと他人をだますような使い方も禁物だ。